Portfolio item number 1
Short description of portfolio item number 1
Posts by Collection
books
portfolio
Portfolio item number 2
Short description of portfolio item number 2
publications
Neural Theorem Proving on Inequality Problems
Published in 5th Conference on Artificial Intelligence and Theorem Proving (AITP), 2020
Paper link
INT: An Inequality Benchmark for Evaluating Generalization in Theorem Proving
Published in The Nineth International Conference on Learning Representations (ICLR), 2021
Paper link
LISA: Language models of ISAbelle proofs
Published in 6th Conference on Artificial Intelligence and Theorem Proving (AITP), 2021
We introduce an environment that allows interaction with an Is- abelle server in an incremental manner. With this environment, we mined the Isabelle standard library and the Archive of Formal Proofs (AFP) and extracted 183K lemmas and theorems. We built language models on this large corpus and showed their effectiveness in proving AFP theorems.
Paper link
Can Network Flatness Explain the Training Speed-Generalisation Connection?
Published in Bayesian Deep Learning Workshop at the Thirty-fifth Conference on Neural Information Processing Systems (NeurIPs), 2021
Paper link
Thor: Wielding Hammers to Integrate Language Models and Automated Theorem Provers
Published in Thirty-sixth Conference on Neural Information Processing Systems (NeurIPS), 2022
Paper link
Autoformalization with Large Language Models
Published in Thirty-sixth Conference on Neural Information Processing Systems (NeurIPS), 2022
Paper link
Magnushammer: A Transformer-based Approach to Premise Selection
Published in arxiv, 2023
What Christian had | What I heard
— Albert Jiang (@AlbertQJiang) March 9, 2023
in mind when he |
suggested the name | https://t.co/Ac7RExnCV9 pic.twitter.com/sVIMiKRafI
Paper link
Draft, Sketch, and Prove: Guiding Formal Theorem Provers with Informal Proofs
Published in The Eleventh International Conference on Learning Representations (ICLR) (Oral), 2023
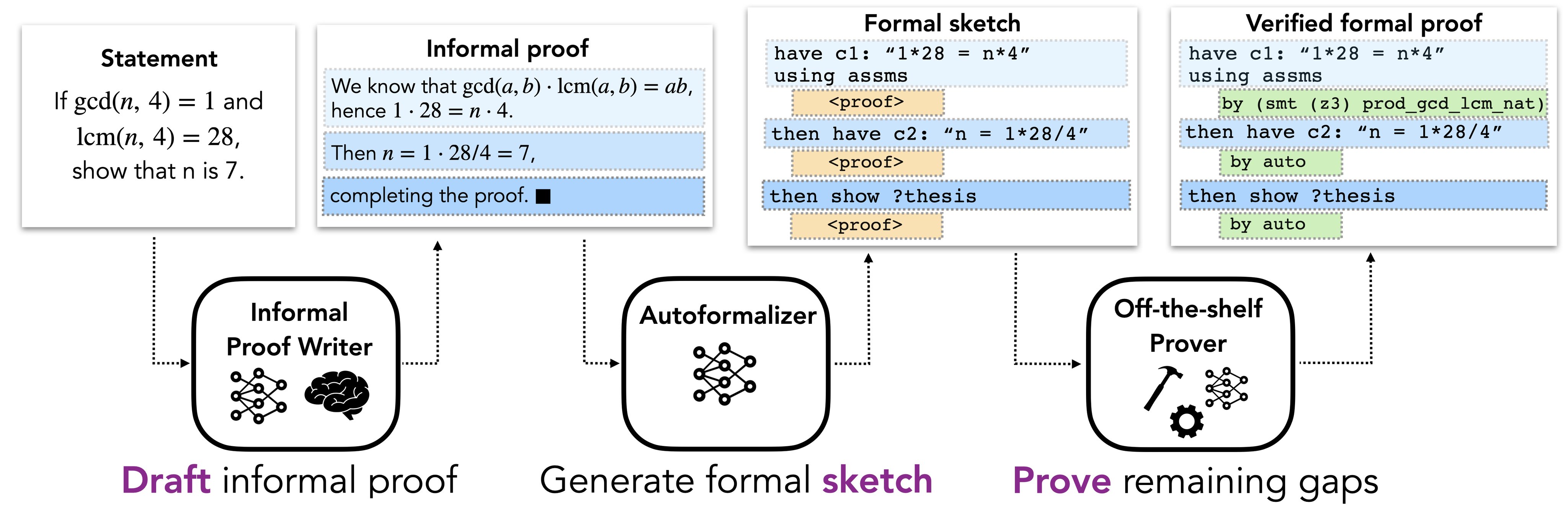
Paper link
Evaluating Language Models for Mathematics through Interactions
Published in arXiv, 2023
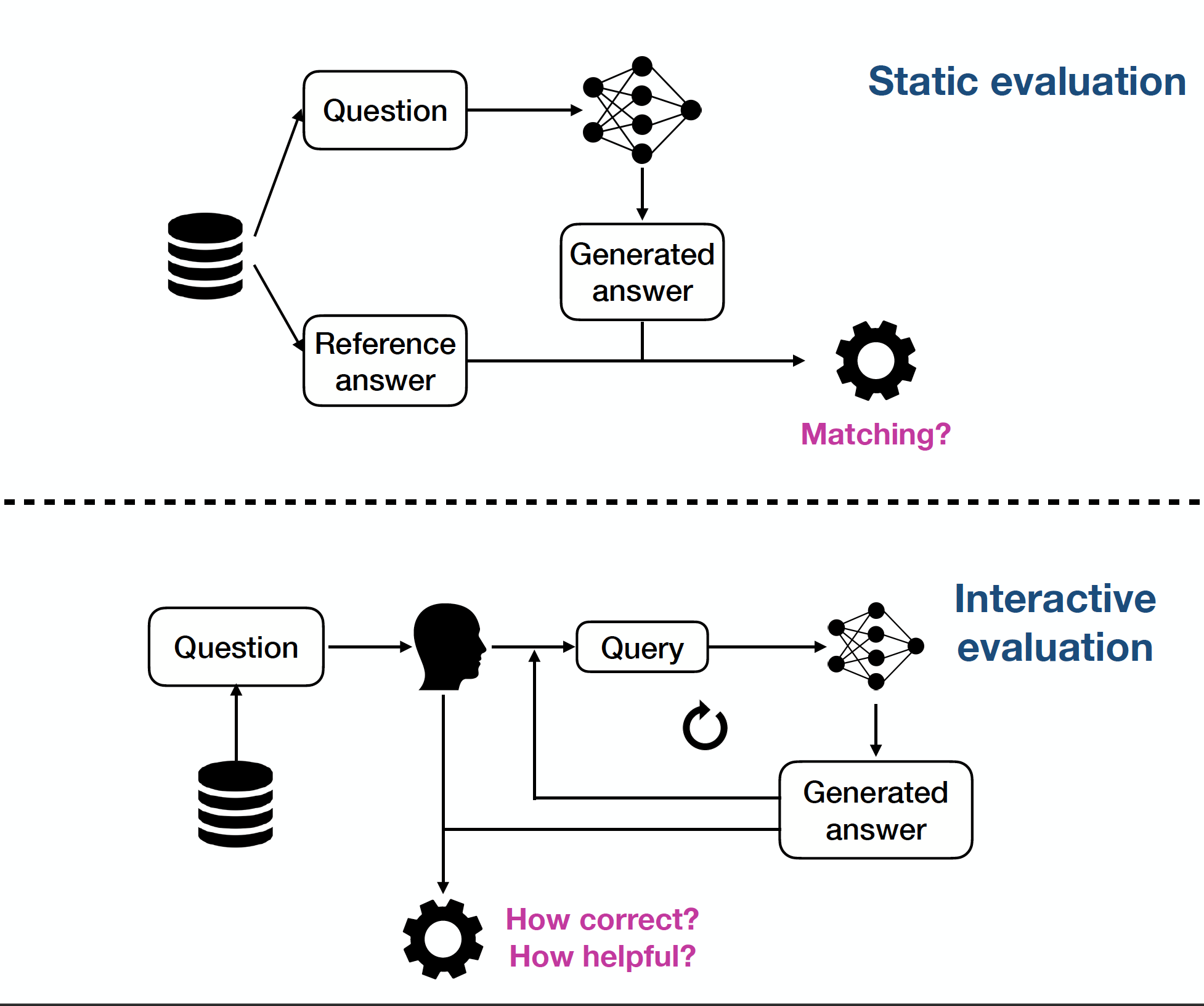
Paper link
teaching
Teaching experience 1
Undergraduate course, University 1, Department, 2014
This is a description of a teaching experience. You can use markdown like any other post.
Teaching experience 2
Workshop, University 1, Department, 2015
This is a description of a teaching experience. You can use markdown like any other post.